Light and Shadows
The spheres used in the proof on the previous page are called Dandelin spheres after the French mathematician Pierre Dandelin (1794 – 1847), who discovered their use,  although the equivalence of the two definitions had been known in some form since the time of Pappus of Alexandria (c.290 – c.350). The line of argument we used in the case of the parabola can be extended to central
conics. In each case, the directrices in the plane P are cut by the planes
through the circles where the Dandelin spheres touch the cone. although the equivalence of the two definitions had been known in some form since the time of Pappus of Alexandria (c.290 – c.350). The line of argument we used in the case of the parabola can be extended to central
conics. In each case, the directrices in the plane P are cut by the planes
through the circles where the Dandelin spheres touch the cone.
If a ball is laid on a table and a bright light shone upon it, the cast shadow has the shape of a conic section. If the light source is above the top of the ball, the shape will be a circle or an ellipse. If it is below the top of the ball, the shape will be one branch of a hyperbola. A parabola results when the light is on a level with the top of the ball. In any case, the point where the ball rests on the table is the focus.  If the circle of the shadow's edge around the ball is projected to a line segment on the table, the extended line will be the directrix. If the circle of the shadow's edge around the ball is projected to a line segment on the table, the extended line will be the directrix.
Or again, if a lamp with a cylindrical lampshade is stood up beside a wall, the edge of the shadow cast on the wall will be the two branches of a hyperbola. If the lamp is tilted so that the light from the top of the shade falls full upon the wall, the resulting shape will be an ellipse.
Conics can be used to model the path of a shadow cast by the sun throughout the day, an observation attributed to Apollonius of Perga (c.262 BC – c.190 BC). The eccentricity of the path is determined by the the latitude θ (the angle made by the ray from the earth's center with the plane of the equator) and the declination δ (the angle made by a ray from the sun with the plane of the equator).
On any given day, the apparent path of the sun in the sky describes a circle. The collection of rays that pass across the tip of a gnomon (an upright set on the ground or some other horizontal surface) forms part of a cone, with the tip as apex. The plane of the ground cuts the opposite nappe of this cone, so that the path of the shadow describes a conic. The angle we've referred to as β is equal to θ, while the angles α and δ are complementary.  The eccentricity of a section cut by in a cone of aperture 2α by a plane with axial angle β is (cos β)/(cos α); so the eccentricity of the shadow's path is (cos θ)/(sin δ). The eccentricity of a section cut by in a cone of aperture 2α by a plane with axial angle β is (cos β)/(cos α); so the eccentricity of the shadow's path is (cos θ)/(sin δ).
For instance, in Uvalde, Texas, the latitude is approximately 29° N. At the winter solstice, when the declination of the sun is approximately 23° S (the latitude of the Tropic of Capricorn), the eccentricity of the path is approximately 2.24, indicating a hyperbola. Its asymptotes are parallel to the orientations of the sun at sunrise and sunset.
The path at any temperate latitude on any day of the year is a hyperbola (or, at the equinoxes, a straight line); above the Arctic Circle, the path describes an ellipse during the days of the midnight sun.
In the diagram shown above, the ray indicates the direction of the sun's light, which determines the angle δ.  The brown figure represents our sundial at noon; its base is horizontal, i.e., parallel to the earth's surface at that point, and perpendicular to the ray from the earth's center. If the edge of the gnomon makes an angle of θ with the surface and lies directly over the noon line, then it stands parallel to the earth's axis. The direction of the shadow cast by the edge at any given time of day is the same every day of the year, independent of the season. This is how most sundials work. The eccentricity of the path traced by the tip of the shadow depends on the sun's declination, however. Click here for the simulation of a sundial on the winter solstice in Uvalde. The brown figure represents our sundial at noon; its base is horizontal, i.e., parallel to the earth's surface at that point, and perpendicular to the ray from the earth's center. If the edge of the gnomon makes an angle of θ with the surface and lies directly over the noon line, then it stands parallel to the earth's axis. The direction of the shadow cast by the edge at any given time of day is the same every day of the year, independent of the season. This is how most sundials work. The eccentricity of the path traced by the tip of the shadow depends on the sun's declination, however. Click here for the simulation of a sundial on the winter solstice in Uvalde.
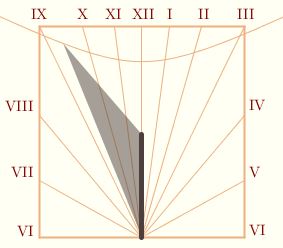 Horizontal sundials are latitude-specific. If you buy a manufactured sundial then it was most likely made for a different latitude, especially if you live where I do; being an out-of-the-way sort of place, it is not the region most sundial-manufacturers have in mind for their marketing strategies. Any sundial can be tipped out of the horizontal to adjust for changes in latitude, however; to do this it is only necessary to determine the latitude for which it was made, which can be done by examining the gnomon or the angles of the hour lines. Sundials of course only indicate local apparent time, with "noon" occurring at the moment shadows are shortest; this changes as you travel from east to west, so your dial may need to be adjusted depending on your location in your time zone and whether or not Daylight Savings Time is in effect. Horizontal sundials are latitude-specific. If you buy a manufactured sundial then it was most likely made for a different latitude, especially if you live where I do; being an out-of-the-way sort of place, it is not the region most sundial-manufacturers have in mind for their marketing strategies. Any sundial can be tipped out of the horizontal to adjust for changes in latitude, however; to do this it is only necessary to determine the latitude for which it was made, which can be done by examining the gnomon or the angles of the hour lines. Sundials of course only indicate local apparent time, with "noon" occurring at the moment shadows are shortest; this changes as you travel from east to west, so your dial may need to be adjusted depending on your location in your time zone and whether or not Daylight Savings Time is in effect.
Isaac Newton observed that a small mirror placed on the sill of a south-facing window can be used to keep time. The sunbeam reflected by the mirror onto the ceiling describes a hyperbolic path; if the situation of the room is good and the ceiling large and marked like a sundial (though in reverse) then this could be used as a very accurate time-keeping device. Newton laid out such a dial on his grandmother's ceiling when he was a boy. The hour lines can be determined empirically by marking the hours on the ceiling on a day in summer and a day in winter, and then connecting the pairs of marks with segments.
There are many other types of sundials, some of which involve conics in other ways. Consult Albert Waugh's Sundials: Their Theory and Construction for detailed, easy-to-follow (but not very theoretical) instructions for making every type of sundial imaginable.
Next: A Touch of Etymology |

