Slicing Cones
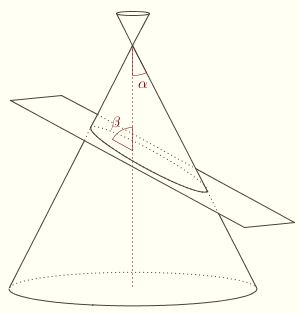 Here we at last touch upon conics as Apollonius of Perga defined them, namely, as sections of cones.
To begin with, a right cone is formed by a circle in a plane and a point (the apex) on the perpendicular line through the center of the circle. The cone is the union of all lines through the apex intersecting the circle. The perpendicular
line is called the axis of the cone, and each line on the cone is called a generatrix of the cone. Notice that the cone extends infinitely in both directions along the axis.
The measure 2α of the interior angle formed by two generatrices coplanar with the axis is called the aperture of the cone.
Given a cone with axis l and apex A, let P be a plane not parallel to l. The measure β of the angle made by l and P (measured in the plane perpendicular to P containing l) will be referred to as the axial angle of the plane.
The intersection between a plane and a cone is called a conic
section. A conic section that contains the apex is called degenerate; otherwise it is called nondegenerate. It should be clear that a degenerate section consists of either a single point (the apex) or two lines intersecting at the apex. Further, we have the following:
- If α < β, then the conic section is a circle (β = 90°) or an ellipse (β < 90°).
- If α = β, then the conic section is a parabola.
- If α > β, then the conic section is a hyperbola.
 Consider the first case. That the section is a circle if β = 90° follows from the Angle-Side-Angle Congruency Condition (which implies that the distance of each point on the section from the axis is equal), so assume that β < 90°.
Let Q be the plane containing the axis l perpendicular to P. Let m be the line where P and Q intersect, and let n and o be the lines where Q and the cone intersect. Let N be the incenter and r the inradius of the triangle formed by m, n, and o. Let O be the excenter that lies on l, and let s be its exradius. The sphere of radius r centered at N and the sphere of radius s centered at O are both tangent to P; let F and G be their points of tangency. It remains to show that the section is an ellipse with foci F and G.
Let C be any point on the section. Note that the generatrix through C is tangent to both spheres. Let P and Q be its respective intersection points.  Now, the triangles CFN and CPN are congruent by the Hypotenuse-Leg Congruency Condition, so CF = CP. Similarly, CG = CQ. So
CF + CG = CP + CQ = PQ
since C is between P and Q. But
PQ = (s – r) cot α
hence is fixed, and independent of the choice of C. So, as C moves around the section, it describes an ellipse with foci F and G.
If α > β , then the plane intersects both "nappes" or halves of the cone. The proof proceeds much as for the ellipse. In this case, one sphere is inscribed in each nappe. If Q is the plane containing l perpendicular to P, the centers of the spheres are excenters for the triangle in Q formed by the cone and P. Their
points of tangency with P are the foci of the hyperbola.
The parabola must be handled differently as it does not admit a two-focus description. Let Q, m, n, and o be as before. Note that m is parallel to one of n and o, say, n. Let O be the point where the bisector of the angle between m and o intersects l, and let r be its perpendicular distance from m. 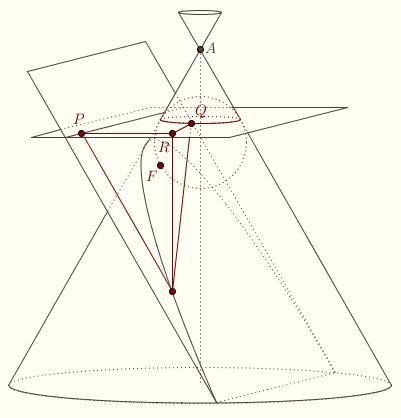 Then the sphere of radius r centered at O is inscribed in the cone and tangent to P at a point F. Let R be the plane containing the circle where the sphere intersects the cone, and let p be the line where P and R intersect. Then the conic section is the parabola with focus F and directrix p.
To see this, let C be a point on the section. Let P be the foot of the perpendicular to p, and R the foot of the perpendicular to R. Let Q be the point where the generatrix through C intersects R. Clearly CF = CQ, since both are tangent to the sphere. Furthermore, the angles PCR and QCR both have measure α, so triangles PCR and QCR are congruent by the Angle-Side-Angle Congruency Condition, and CP = CQ = CF.
Next: Light and Shadows |
