The Structure of the Hyperbola
 After studying the structure of ellipses, we turn now to hyperbolas.
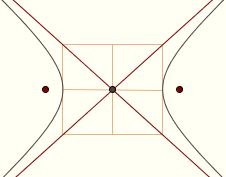
To begin with, there exist two lines through the center of a hyperbola, called asymptotes, which approach the hyperbola arbitrarily closely without intersecting it. These asymptotes contain the diagonals of the rectangle given by the major and minor axis.
To see this, use the auxillary circle as eccentric circle. Note that the two tangents from the focus F to the circle intersect the circle on the directrix. Each line from the center O through a point of tangency therefore intersects at no point.
If E is a point on the auxillary circle in the opposite half plane of the directrix from F, 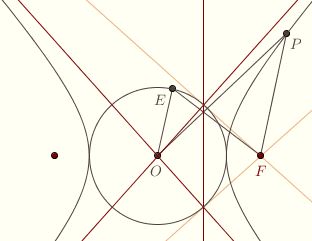 then the resulting point P on the hyperbola is less distant from the corresponding asymptote than E. Therefore, as E approaches the point of tangency, P approaches the asymptote, and OP increases without bound. Click here for an animation.
Many of the ideas we developed concerning ellipses have their counterparts in the world of hyperbolas. For instance, recall that, given two points F and G, we can conceive of an ellipse with foci F and G as the locus of points C such that CF + CG is some fixed constant. There is an analogous two-focus description of the hyperbola. Namely, given the hyperbola with foci F and G, directrices l and m, and eccentricity ε > 1, the difference |CF – CG| is constant for any point C on the hyperbola, and equal to ε times the distance between the directrices.
To see this, let x be the perpendicular distance between the directrices. Given a point C on the hyperbola, let r be the distance to l and s the distance to m. The point C lies outside the region contained by the directrices, so |r – s| = x. On the other hand, we know that CF = ε ⋅ r and CG = ε ⋅ s, so
|CF – CG| = |ε ⋅ r – ε ⋅ s| = ε |r – s| = ε ⋅ x
This allows us to sketch hyperbolas using the same graph paper we used for ellipses. Using paper with a grid spacing of 24 units between the foci, we could, for instance, construct the hyperbola that crosses the major axis 4 units from one focus and 20 from the other, for each of the two foci. The difference is 16. For every circle we move out from one focus, we need to move one out from the other, so that the difference remains 16. So we plot points at the 5th and 21st circles, and the 6th and 22nd, and so on. This hyperbola has eccentricity 12/8 = 3/2 because the semiminor axis is 8 and the linear eccentricity is 12 (as it is for all hyperbolas using this graph paper).
Shown here are the hyperbolas with eccentricities 3/2, 2, and 4. Graphing hyperbolas on this paper is like graphing lines with slope 1.
Hyperbolas also obey something like the reflective property for ellipses. Namely, the line tangent to a point on a hyperbola is the bisector of the angle formed by the two focal radii from the point. We can prove this through an optimization problem, as we did with the ellipse, but let's explore another method instead.
Let C be a point on the hyperbola, and let m be the line tangent at C. Let X and Y be the points of intersection with the two directrices, let A and B be the feet of the perpendiculars from C to the directrices. Then CF/CA = CG/CB, since both equal the eccentricity. 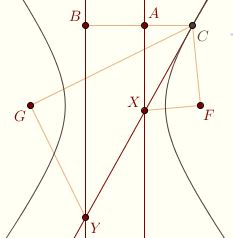 On the other hand, the triangle CAX is similar to the triangle CBY, so CA/CX = CB/CY. It follows that CF/CX = CG/CY. Now, CFX is a right angle, since the eccentric circle (for F and its directrix) centered at C passes through F, and therefore XF must be tangent to the circle at F, hence perpendicular to the radius CF. The angle CGY is right as well. So the triangles CFX and CGY are similar. The angles FCX and GCY are therefore congruent, and m bisects FCG.
From this it follows that the tangents at the point of intersection between an ellipse and a hyperbola with the same foci are always perpendicular. Now, the family of confocal ellipses for a fixed pair of foci is a set of disjoint curves whose union is the
entire plane excluding the segment between the foci. Likewise the family of confocal hyperbolas.
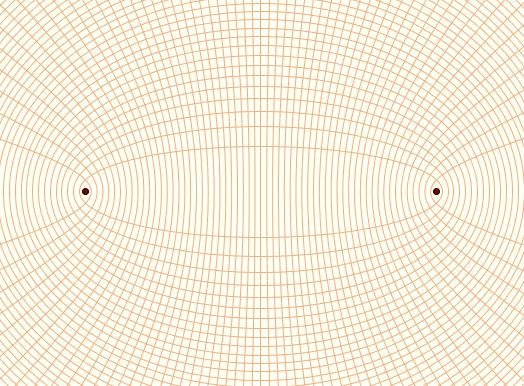
We've just established that each curve in the family of ellipses is orthogonal to each curve in the family of hyperbolas; they therefore form orthogonal families.  Unlike the other "graph papers" we've considered, in this graph paper, the grid lines always meet at right angles; the "lines" with slope ±1 are circles centered at the foci.
The hyperbola also admits a pedal construction. In this case, each tangent from a focus to the auxillary circle is perpendicular to a tangent of the ellipse at the point of intersection with the circle. Click here for an animation of the hyperbola as an envelope of tangent lines.
Next: Slicing Cones |
