Eavesdropping with Ellipses
The Shortest Path Problem is an early optimization problem that appeared in Heron's On Mirrors, a Greek text on optics. Given two points A and B on the same side of a line m, what is the shortest straight-line path from A to m to B?
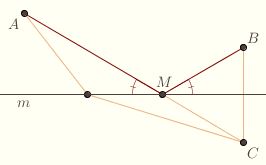 Let C be the reflection of B across m. Suppose M is some point on m. Notice that the triangle MBC is isosceles, so that MB = MC.
The Triangle Inequality states that the shortest route between two points is always along the line segment joining them, implying that AM + MC ≥ AC, with equality if and only if M is between A and C. So the distance from A to M to C is minimized precisely when M is between A and C. It follows that the distance from A to M to B is also minimized when M is between A and C.
Taking this point as our M, note that the angles made by BM and CM with m are equal, since m is the perpendicular bisector of BC.  Also, the angles made by AM and CM with m are equal, since they're vertical angles. So AM + MC is minimized precisely when the angles made by AM and BM with m are equal.
Now consider an ellipse with foci F and G. Let C be a point on the ellipse, and let m be the line at C making angles of equal measure with the focal radii.
Suppose M is a point on m. Heron's Problem implies that the straight-line path of minimal distance from F to m to G has vertex C. Therefore every point on m not equal to C is in the exterior of the ellipse. So m is tangent to the
ellipse at C.
 There's an old story, repeated in many books, that the statesman John Quincy Adams would eavesdrop on other politicians through making use of the elliptical shape of the Statuary Hall in the Capitol. Apparently this is only a myth, but the principle is sound enough. If two persons
stand in an elliptical hall, one on each focus, then they can whisper to one
another even in the midst of background noise and intervening objects.
Click here for a demonstration. Notice how the trace of the wavefronts reproduces the elliptic graph paper discussed on the previous page.
The same idea is used in some document scanners. A source of illumination runs along the focal line of a reflector shaped like an elliptical cylinder; 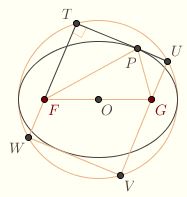 the reflector then focuses the light in a parallel line across the paper.
We can use the reflective property of the ellipse to construct it as an envelope of tangents, much as we did for the parabola, except that now we use the auxillary circle rather than the tangent line at the vertex. Namely, the line from a focus to a point on the auxillary circle is perpendicular to a tangent of the ellipse at the point of intersection with the circle.
To see this, let T be a point on the auxillary circle, and construct the rectangle TUVW circumscribed by the auxillary circle. The diagonals are diameters of the circle, so TV = 2a = UW, where a is the semimajor axis of the ellipse, i.e., the radius of the circle. Let P be the point on TU so that FP is parallel to WU. We claim that P is on the ellipse, 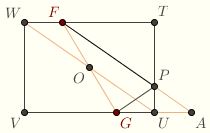 and that TU is tangent to the ellipse at P, but this is something we need to prove.
Let A be the point where FP intersects VU. The quadrilateral FAUW is a parallelogram, so FW = AU. On the other hand, OF = c = OG by construction, where c is the linear eccentricity, and OW = OU since O is the center of the circle. So the triangle OFW is congruent to the triangle OGU by the Side-Angle-Side Congruency Condition. It follows that GU = FW = AU, hence that the triangle GPU is congruent to the triangle APU by Side-Angle-Side. Therefore
PF + PG = PF + PA = UW = 2a
So P is on the ellipse with foci F and G and eccentricity c/a. On the other hand, the angles FPT and BPU have equal measure, so TU must be tangent at P.
Thus, in order to construct a tangent to the ellipse,we have only to construct a line from a focus through the auxillary circle, and then the perpendicular to this line at the point of intersection with the circle.
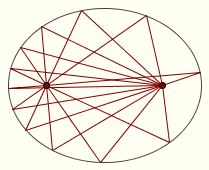
 This is easily done on paper. Begin by constructing a circle with a compass. Choose an arbitrary point F between the center O and the perimeter for a focus. Place a right angle such as a drafting triangle or an index card with one leg across the focus and the corner on the circle; then trace the other leg with your pencil. Repeat as many times as desired.
To obtain a better picture, locate the other focus G by intersecting the line OF with the circle centered at O passing through F and repeat the same process for G.
This is known as the pedal construction of the ellipse. Click here for an animation.
Next: The Structure of the Hyperbola |
