Tacks and Cardboard
Consider the ellipse with foci F and G, directrices l and m, and eccentricity ε < 1. Let x be the perpendicular distance between the directrices.
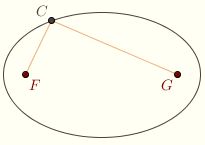 Now let C be any point on the ellipse. Let r be the perpendicular distance to l, and s the perpendicular distance to m. We know that CF = ε ⋅ r and CG = ε ⋅ s, so
CF + CG = ε ⋅ r + ε ⋅ s = ε (r + s) = ε ⋅ x
It follows that the sum CF + CG is independent of C, and is in fact equal to 2a, where a is the semimajor axis. Thus, an alternative definition of the ellipse would be this: an ellipse with foci F and G is a locus of points C such that CF + CG is equal to some fixed number. Click here for an animation.
This is of course what allows for the two-focus construction of the ellipse.
Place a sheet of paper on a piece of cardboard and drive two pins through
the paper. The pins should have a piece of thread tied around their points.
Stretch the thread taut with the point of a pencil and trace around the pins. The eccentricity of the ellipse constructed is the ratio of the pin spacing to the string length. So, if you place your pins (say) 7 cm apart, and use a string 10 cm long, then the ellipse you trace will have eccentricity 7/10.
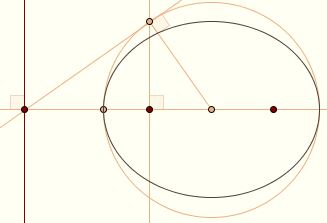 If your construction of the ellipse is suffciently accurate, you can construct the directrix as follows. Let F and G be
the foci, i.e., the holes in the paper. Construct the line FG. Use a ruler to locate the center O (the midpoint of FG), and construct the auxillary circle with a compass. Use a right angle such as a drafting triangle to construct the perpendicular to FG at F. Let X be its point of intersection with the auxillary circle. The perpendicular to OX at X is the tangent to the circle at X; this tangent is concurrent with the axis and directrix. So the perpendicular at the point of intersection is the directrix.
As we noted above, the eccentricity is the ratio of the distance between the pins to the length of the string. You can verify this by choosing any point on the ellipse, measuring the distance to F and the perpendicular distance to the directrix, and computing the ratio. If your measurements are accurate to the nearest millimeter, the ratios should in agreement to within one tenth or so.
Ellipses can be sketched using circular "graph paper." Beginning with a pair of foci F and G a certain whole number of units apart, construct a sequence of circles with whole-number radii at each focus. For instance, we could choose the foci to be 24 units apart, and then, at each focus, construct circles of radius 1, 2, 3, and so on. From each intersection point in the grid that results, the distance to each of the foci is given by the circle spacing. For instance, if a point lies at the intersection between the 17th circle from F and the 13th circle from G, then the combined distance is 17 + 13 = 30. Every other point C on the ellipse passing through this point must also satisfy CF + CG = 30. So we can plot points at the intersection of the 16th and 14th circles, and the 18th and 12th circles, and so on. This ellipse crosses the axis 3 units beyond each focus, at the intersection of the 3rd and 27th circles. It has eccentricity 24/30 = 5/6.
Or again, we could sketch the ellipse that crosses the axis 5 units beyond each focus. This ellipse would have eccentricity 24/34 = 12/17.
In general, as we trace any ellipse, for each circle we move out from F, we move in one circle toward G, and vice versa. It's a bit like we're graphing lines with slope –1. As an exercise, try sketching the ellipses described above, as well as ellipses with eccentricity 6/7, 3/4, 2/3, 1/2, and 4/9. Graph paper is provided here for your convenience.
Be careful not to confuse this method with our other graph-paper method, which uses a fixed focus and directrix. Under the two-focus construction, each ellipse has a different directrix. As the intersection point with the axis moves further and further away from the focus, the ellipse becomes more and more "circular," and the eccentricity tends to 0. As the point moves closer and closer to the focus, the ellipse approaches the line segment between the foci, and the eccentricity tends to 1.
Next: Eavesdropping with Ellipses |
