Conic Sections

The Area of an Ellipse

The key to computing the area of an ellipse is to relate it to its auxillary circle. 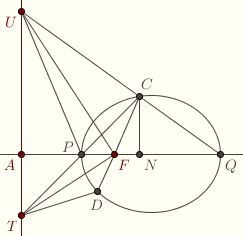Namely, given an ellipse with semimajor axis a and semiminor axis b, the perpendicular distance from the major axis to a point on the auxillary circle is a/b times the distance from the major axis to the intervening point on the ellipse.

Consider an ellipse with focus F, directrix l, and vertices P and Q. Let C be a point on the ellipse. Let T and U be the respective points where CP and CQ intersect l. Then PF/CF = PT/CT. It follows that FT bisects the angle PFD, where D is the other endpoint of the chord from C through F. On the other hand, QF/CF = QU/CU, so FU bisects PFC. It follows that TFU is a right angle. Therefore AF is the geometric mean of AT and AU, i.e., AF² = AT ⋅ AU.

Now let N be the foot of the perpendicular from C to the axis. Then PNC is similar to PAT, so CN/PN = AT/AP. Similarly, CN/QN = AU/AQ. So

CN²/(PN ⋅ QN) = AF²/(AP ⋅ AQ)

which is a fixed ratio, independent of C. If C is on the minor axis, then this is seen to be b²/a², so this is the value in general.

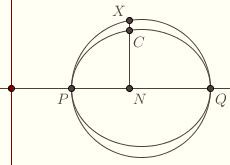
Let X be the point on the auxillary circle so that C is between X and N. Then the triangle PXQ is a right triangle, since it is inscribed in a semicircle, so XN is the geometric mean of PN and QN. It follows that PN ⋅ QN = XN², hence CN²/XN² = b²/a². So the ratio of CN to XN is b/a.

The area of the ellipse can thus be related to the auxillary circle as follows. Inscribe in the circle a regular 2n-gon with vertices at the endpoints of the major axis. 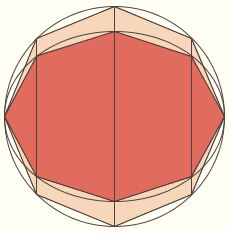Use this to inscribe a 2n-gon in the ellipse, such that each vertex on the latter lies on the perpendicular from a vertex of the former to the major axis. The distance between each pair of vertices on the 2n-gon inscribed in the ellipse is b/a times the distance between each pair of vertices on the regular 2n-gon. It follows from the area formulas for the triangle and the trapezoid that the area of the 2n-gon in the ellipse is b/a times the area of the regular 2n-gon. The area of the latter approaches πa² as n increases, so the area of the latter approaches πa² ⋅ b/a = πab.

We've proved that the area of an ellipse with semimajor axis a and semiminor axis b is πab.

We can also relate the area of the ellipse to the area of the parallelogram given by a pair of conjugate diameters. Let m be the line containing the major axis, and consider the one-to-one correspondence which sends a point P to the point on the perpendicular from P to m whose distance from m is b/a times that of P. This yields a one-to-one correspondence between the auxillary circle and the ellipse. Furthermore, it perserves parallel lines and relationships of distances along lines. Click here for a demonstration.

A pair of conjugate diameters in the ellipse are thus paired with a pair of diameters in the circle with the property that every chord parallel to one is bisected by the other. It follows that the diameters on the circle are perpendicular. The tangents at the endpoints of one diameter are parallel to the other, so the same is true of the ellipse. This establishes that the tangent at the endpoint of a diameter is parallel to its family of chords. The tangents on the circle form a square whose area is 4a². So the area of the parallelogram circumscribing the ellipse is 4a² ⋅ b/a = 4ab.

In particular, the area of every parallelogram given by a pair of conjugate diameters has equal area, and this area is the area of the rectangle given by the major and minor axes. Click here for a demonstration.

Incidentally, this is cited as a lemma in Section I.2 of Newton's Principia, where he considers the centripetal force acting on a body moving in an ellipse. He there notes that if the the center were moved to infinity then the trajectory would become parabolic and his theorem would resolve into one proved by Galileo. It's worth perusing classic works on mechanics like Kepler's Epitome of Copernican Astronomy, Galileo's Dialogues Concerning the Two New Sciences, and Newton's Principia. They approach geometry from the synthetic point of view, as we are here.

Next: Tacks and Cardboard