Conic Sections

Central Conics

A central conic is a conic with eccentricity ε ≠ 1 (an ellipse or a hyperbola).

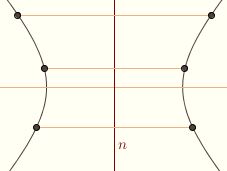Every conic is symmetric with respect to its axis; this is a simple consequence of the definition. But you may also have noticed that hyperbolas and ellipses appear to possess another kind of symmetry.

To verify this, consider a central conic with focus F, directrix l, and eccentricity ε. We've established that the diameter given by the family of chords parallel to the axis is perpendicular to the axis. Let n be the line containing the diameter. We wish to show that the conic is symmetric with respect to n.

Every line perpendicular to n intersects the conic once, twice, or not at all. If such a line intersects twice, the resulting chord belongs to the family of chords bisected by n. On the other hand, if such a line intersects once, it does so precisely on n, and the conic is an ellipse.

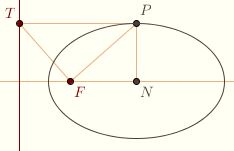To see this, suppose P is such a point of intersection. Let N be the foot of the perpendicular to the axis, and T the foot of the perpendicular to the directrix. We know that PF is perpendicular to TF for, if it were not, we could reverse the argument wherein we showed that no line intersects a conic more than twice to produce a second intersection point. So PFT is a right triangle. Thus PT < PF, since the hypotenuse is less than each leg, and the conic is an ellipse. Furthermore, PFT is similar to FNP, so NF/PF = ε.

It remains to be shown that P lies on the diameter. The diameter must intersect the ellipse at a point Q in the same half plane of the axis as P, and the perpendicular to the directrix must intersect the conic only at Q (since otherwise n must bisect the chord). 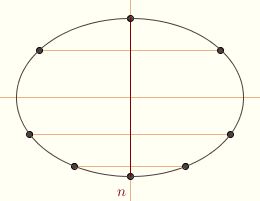An argument similar to the above shows that OF/QF = ε, where O is the intersection point between n and the axis, and hence that FNP is similar to FOQ. So F, P, and Q are collinear. Any line through F intersects the ellipse in at most two points, and F must lie between these points, so P = Q.

Every line perpendicular to n must therefore either contain a chord bisected by n, intersect the conic exactly once on n, or not intersect the conic at all. So n really does serve as a line of symmetry. Let G be on the axis so that O is the midpoint of FG, and let m be the perpendicular to the axis so that l and m are equidistant from n. Then the conic coincides with the one given by the focus G, directrix m, and eccentricity ε.

We're now ready to introduce some of the traditional terminology. The midpoint O of the two foci F and G is called the center of the conic (hence the term, central conic). If P and Q are the two vertices, then the circle with diameter PQ is called the auxillary circle of the conic. The chord PQ is called the major axis. The length a = OP is the semimajor axis, and c = OF is the linear eccentricity. Note that c/a = ε.

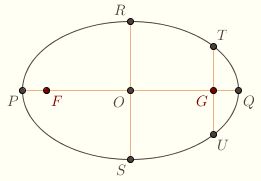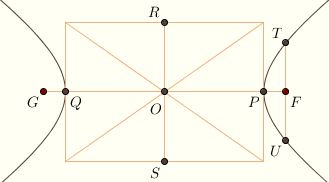
In an ellipse, the diameter RS given by the major axis called the minor axis, and the length b = OR is called the semiminor axis. It satisfies b² = a²– c².

In a hyperbola, the semiminor axis is defined by the equation b² = c²– a², and the minor axis RS is the segment through O perpendicular to the major axis such that OR = b = OS.

In either case, the chord TU through the focus perpendicular to the axis is called the latus rectum.

In the case of the parabola, we saw that every diameter is parallel to the axis. A related theorem for the case of central conics asserts the following: if one diameter bisects the family of chords parallel to a second, then the second bisects the family of chords parallel to the first. To see this, note first that the arguments above imply that every diameter of a central conic passes through the center O. Let n be the line containing a diameter, and let m be the diameter given by the family of chords parallel to n.

The conclusion is obvious if either m or n is parallel to the directrix, so assume that neither is. Let m and n meet the directrix and T and U, respectively. 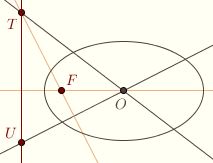We've shown that FT is perpendicular to n. Therefore FT and the axis are both altitudes of triangle OTU, so F is the orthocenter of the triangle. So FU must be perpendicular to m, and n is the diameter for the chords parallel to m.

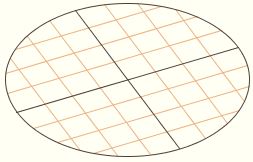
So diameters come in pairs. Diameters related like this are called conjugate pairs. Click here for an animation of the conjugate diameters of an ellipse; click here for an animation of the conjugate diameters of a hyperbola. The diameters are shown in red, and each family of parallel chords is shown in orange.

Next: The Area of an Ellipse