Conic Sections

The Quadrature of the Parabola

In the third century before Christ, Archimedes (c. 287 BC – c. 212 BC), the great Greek mathematician, physicist, astronomer, inventor, and engineer, computed the area of the region bounded by a parabola and one of its chords. His argument is of historical interest because it anticipates the development of integral calculus by almost two thousand years.

To begin, we first prove that the tangent at the endpoint of a diameter is parallel with the family of chords giving rise to the diameter, and that the extension of the diameter is concurrent with the pair of tangents at the endpoints of each chord. Furthermore, the endpoint of the diameter is the midpoint of the median of the resulting triangle, and the tangent at the endpoint bisects the two other sides.

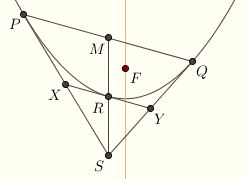
Given a chord PQ on the parabola with focus F and directrix l, let S be the intersection point between the tangents at P and Q. Let M be the midpoint of the chord PQ. Let A be the foot of the perpendicular from P to l, and B the foot of the perpendicular from Q to l.

Consider the triangle ABF. Our arguments on the last page show that PS is the perpendicular bisector of AF and that QS is the perpendicular bisector of BF. The perpendicular bisectors of the sides of a triangle are concurrent at the circumcenter, so the perpendicular from S to l bisects AB. It follows that the perpendicular bisects PQ as well, since these are the legs of a trapezoid. So MS is the perpendicular, hence is parallel to the axis and therefore contains the diameter. Let R be the endpoint of the diameter.

The same argument applies to triangle PRX, where X is the intersection point between the tangents at P and R. So the median of PRX through X is parallel to RS. The Midsegment Theorem therefore implies that X is the midpoint of PS. Similarly, the point Y where the tangents at Q and R intersect is the midpoint of QS. 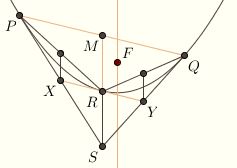It follows from the Midsegment Theorem that XY is parallel to PQ, and R is the midpoint of MS.

The triangle PQS bounded by a chord PQ and the tangents at the endpoints of the chord is called an Archimedean triangle for the parabola. In his short book The Quadrature of the Parabola, Archimedes establishes that the area of the segment contained by the chord and the parabola is two-thirds the area of the Archimedean triangle given by the chord.

First, note that the area of triangle PQR is 1/2 ⋅ AB ⋅ MR. On the other hand, the area of PQS is 1/2 ⋅ AB ⋅ MS. It follows that the area of PQR is half the area of PQS. By a similar argument, PUR is half the area of PXR, and QVR is half the area of QYR. 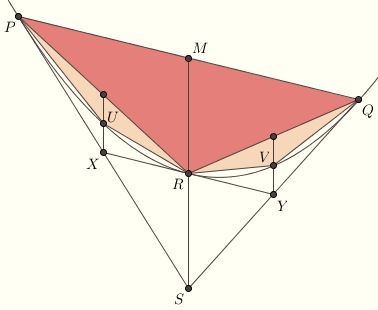The areas of PUR and QVR therefore sum to one-eighth the area of PQS. Our approximation of the area is therefore

1/2 ⋅ (1 + 1/4)

times the area of PQS. We continue in this fasion, approximating the parabolic segment more and more closely with triangles. The limit of these approximations is k times the area of PQS, where

k = 1/2 ⋅ (1 + 1/4 + 1/4² + ⋯)

If we set

x = 1 + 1/4 + 1/4² + ⋯

then

1/4 ⋅ x = 1/4 + 1/4² + 1/4³ + ⋯ = x – 1

So x = 4/3, and k = 2/3. It follows that the area of the segment is two-thirds the area of PQS, as was claimed.

Next: Central Conics