Conic Sections

Sunbeams and Satellite Dishes

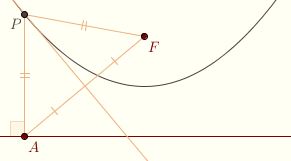Recall that a point P is on the parabola with focus F and directrix l if and only if PF/PA = 1, where A is the foot of the perpendicular to l. In other words, PF = PA, and P is equidistant from F and l.

It follows that the construction of a point on the parabola with a compass and straightedge is relatively straightforward. Given a point A on the directrix, construct the perpendicular to l at A. The point P is equidistant from A and F, hence lies on the perpendicular bisector of FA. So P lies at the intersection of these two lines. Click here for an animation.

Each diameter of a parabola is parallel to its axis. To see this, let PQ be a chord and M its midpoint. Let X be the foot of the perpendicular from F to the chord, and let T be the intersection point between XT and l. 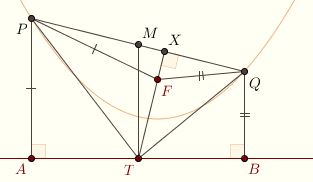We've seen that the diameter given by PQ lies on MT. Let A and B be the feet of the respective perpendiculars from P and Q to l. The Pythagorean Theorem implies that

AT² = PT²– PA²

Furthermore, PXT and PXF are right triangles as well, so, substituting,

PT² = PF² – XF² + XT²

On the other hand, PA = PF by definition, so

AT² = XT² – XF²

Similarly,

BT² = XT² – XF²

It follows that AT = BT, and T is the midpoint of AB. So MT is the median of the trapezoid ABQP, hence is parallel to the bases and to the axis of the parabola. Click here to view an animation of the diameter; the axis is shown in orange, the diameter in red.

Based on the picture at the top of the page, you may have guessed that the altitude of the isosceles triangle PAF is tangent to the parabola at P. To see this, suppose that Q is any other point on the perpendicular bisector of FA. Let B be the foot of the perpendicular from Q to l. The shortest distance from Q to l is along the perpendicular, so QB < QA. On the other hand, Q is equidistant from F and A, so QF = QA. It follows that QB < QF, and Q is in the exterior of the parabola.

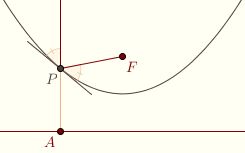This leads to one of the most famous and important properties of the parabola, namely, that the diameter and the focal chord to the endpoint of the diameter form congruent angles with the tangent at the point. This is because the altitude of an isosceles triangle bisects the angle, while vertical angles have equal measure. So the angle made by the diameter and the tangent is equal to the angle made by PA and the tangent, hence to the angle between the tangent and PF.

This is of course the principle behind satellite dishes. A satellite dish is in the shape of a paraboloid of revolution, obtained by revolving a parabola about its axis. Waves traveling parallel to the axis from a distant source strike the surface of the dish and bounce off, concentrating the signal at the focus, which is where the feed antenna is placed. Click here for a demonstration.

There is an ancient legend that the Greek mathematician Archimedes designed parabolic reflectors during the siege of Syracuse, to focus sunlight and set the ships of the enemy on fire. This is now thought apocryphal, but the idea is sound enough. The reflectors behind car headlights are shaped like paraboloids with the light source at the focus; this directs the light beams straight ahead of the car. Telescope reflectors are also in the shape of paraboloids. Liquid mirror telescopes employ a rotating circular vat of liquid metal: under the influences of gravity and centrifugal force, the liquid climbs the sides of the vat, forming a parabolic surface. Such telescopes can only be directed upward, of course.

The same principle can be used to concentrate sound waves. If two satellite dishes are positioned vertically, facing each other, then a person whispering into one dish can be heard at the focus of the other. When I was a freshman in high school, my algebra teacher asked me to find him a pair of dishes, having seen the demonstration at the Exploratorium in San Francisco. Much to his surprise, I was able to acquire a large fiberglass dish in a short amount of time, thanks to my father's military contacts. He wasn't ready for it, so it languished in the backyard for three years. I had the same teacher for calculus when I was a senior and he asked if I still had the dish. My father and I disassembled the dish into two pieces and I took it to school in my truck. Then our class stood the halves up on desks at opposite ends of the library and whispered to one another. It worked, and everyone was amazed.

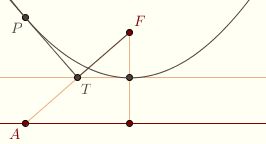I also once encountered a pair of receivers like this in a park. Apparently no one knew what they were for, and a small tree had even grown up between them. But they still worked, the noise of the busy playground notwithstanding.

We have seen how to construct points on the parabola using only a compass and straightedge. We can also construct the parabola as an envelope of tangents. The key observation is that the focal line to a point on the line tangent at the vertex is perpendicular to the tangent through that point. To see this, let T be a point on the tangent at the vertex, and let A be the point where FT intersects the directrix. The tangent at the vertex is parallel to the directrix, so the Midsegment Theorem for triangles shows that T is the midpoint of FA. Let P be the point where the perpendicular to the directrix at A intersects the perpendicular bisector of FA. Then P is on the parabola, and PT is tangent to the parabola at P.

This is what admits the pedal construction of the parabola. It's easy to explore with pencil and paper as follows. Starting with the focus and the line tangent at the vertex, use a drafting triangle to construct a right angle for each point on the line, with one leg passing through the focus; the other leg of the angle will then be tangent to the parabola.

Next: The Quadrature of the Parabola