Parabolas and Artillery
Now that we've established the main properties and applications of conic sections known to the ancients, let's consider some results from the post-classical period.
 In 1638, while under house arrest, Galileo published his Two New Sciences, a landmark text on mechanics. At the beginning of Book III he defines uniform motion to be motion in which the distances traversed by a particle during any equal intervals of time are themselves equal; uniformly accelerated motion he defines as motion under which, when an object starts from rest, its momentum receives equal increments in equal times.
The first may be conceived of as straight-line motion with constant speed; the second as that of a falling object. The latter went against the commonly received notion, which said that the momentum of a falling object is proportional to the distance traversed, so that an object falling twice as far strikes the ground twice as hard and moving at twice the speed. Galileo shows this to be contrary to reason and experience.
Galileo further postulates that the speeds acquired by the same body rolling down inclined planes of different grades are equal when the elevations of the starting points are equal. After discussing the reasonableness of this postulate he establishes his most important theorem, namely, that the distance traversed by a body falling from rest with a uniformly accelerated motion is proportional to the square of the elapsed time, or d = c ⋅ t2 for some constant c. So, if a body falls a certain distance in one second, then it falls four times as far in two seconds, and nine times as far in three seconds, and so on.
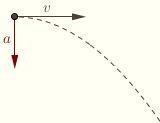 After developing various applications of this law through the remainder of Book III, Galileo proceeds to Book IV, where he states the result that concerns us here, namely, that a projectile subject to a uniform horizontal motion compounded with a naturally accelerated vertical motion moves in a parabolic trajectory. For instance, in the picture shown to the right, an object (say, a cannonball) is given an initial velocity of v in the horizontal direction. The horizontal component of its motion retains this velocity; the vertical component is subject to the uniform acceleration of gravity.
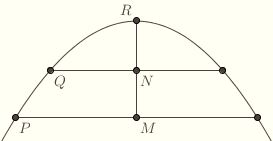 He begins with the following result from Apollonius. Suppose P and Q are two points on a parabola, and let M and N be the points where the respective chords perpendicular to the axis intersect the axis. Let R be the vertex. Then
MP2/NQ2 = MR/NR
To see this, consider the parabola as a section of a cone. Let AB be the diameter of the circular section containing MP and perpendicular to MP, and CD the diameter of the circular section containing NQ and perpendicular to NQ. 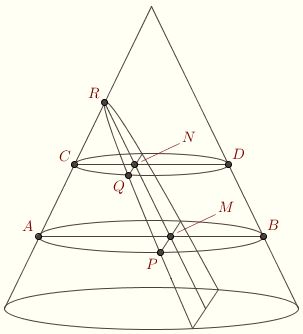 The triangle APB is inscribed in a semicircle, so the angle at P is a right angle and MP is the geometric mean of AP and BP. Thus MP2 = AM ⋅ BM. Similarly, NQ2 = CN ⋅ DN. Furthermore, MNDB is a parallelogram, so DN = BM. It follows that
MP2/NQ2 = (AM ⋅ BM)/(CN ⋅ DN) = AM/CN
Next, the triangles ARM and CRN are similar, so AM/CN = MR/CR. Substition obtains the result.
This is equivalent to saying that the vertical distance to the vertex is proportional to the square of the horizontal distance to the axis, which amounts to the description of parabolas you're probably most familiar with, i.e., as graphs of equations like y = ax2 on the xy-plane. For, if the point P with coordinates (x,y) is on the parabola given by y = ax2, then x = MP and y = MR, so that MR = a ⋅ MP2.
If we imagine firing our cannonball in the horizontal direction with initial velocity v, then its horizontal distance from the gun at time t is v ⋅ t. On the other hand, the vertical distance is c ⋅ t2, as noted above. 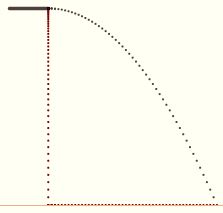 Putting these together, we find that the vertical displacement is proportional to the square of the horizontal displacement:
dv = (c/v2) ⋅ dh2
It follows that the projectile follows a parabolic trajectory.
Click here for a demonstration. Notice how the horizontal component of the velocity remains constant, while the vertical component increases proportionally with time. So, if after a certain unit of time the ball is dropping at a certain rate, then, after twice as much time, it will be dropping at twice the rate, and so on.
If, instead of leveling the gun straight ahead, we fire at an angle, the path of motion remains parabolic, but the vertical component of the initial velocity causes the ball to move up before moving down.
Galileo's laws of mechanics anticipate Newton's laws of motion and gravitation, which appeared later in the seventeeth century. It was Galileo who said:
Philosophy is written in that great book which ever lies before our eyes — I mean the universe — but we cannot understand it if we do not first learn the language and grasp the symbols, in which it is written. This book is written in the mathematical language, and the symbols are triangles, circles and other geometrical figures, without whose help it is impossible to comprehend a single word of it; without which one wanders in vain through a dark labyrinth.
Next let's see how conic sections can be used to model the motion of the planets.
Next: Planetary Motion |
