Conic Sections

Planetary Motion

The Almagest of Claudius Ptolemy (c.90 – c.168), a Greco-Roman mathematician, astronomer, and geographer, was the standard text on cosmology for well over a thousand years. It models the universe using a geocentric, or earth-centered, system with a spherical earth and circular orbits.

So, for instance, the planet Jupiter might be conceived of as moving in a circle around the earth at a constant rate. This rate is measured against the field of stars. Every night Jupiter rises in the east and sets in the west together with the other heavenly bodies. On any particular night its position against the field of stars appears unchanged to the naked eye. Its position does change as time goes on, however: in general, it moves across the star field from east to west. The same is true of the other planets; Saturn is slow, while Venus and Mercury are fast.

However, ancient astronomers observed that Jupiter and the other planets seem to move backward periodically, a phenomenon known as retrogression. The Ptolemaic model corrected for this by including epicycles, an idea first proposed by Apollonius of Perga. The epicycle is a small circle that moves along a larger circle called the deferent. 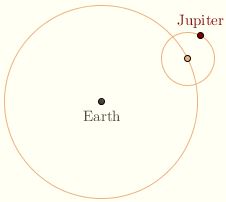The deferent is centered at the earth; it thus represents the simple circular orbit. As the imaginary epicycle moves along the deferent, the planet moves around the epicycle. To an earth-based observer, this causes it to speed up and slow down and, occasionally, to move backward against the field of stars. Also, its distance increases and decreases periodically, another observed phenomenon.

Click here for an animation. The outer circle represents the fixed sphere of the stars.

Ptolemy's model was regarded as trustworthy for over a thousand years. It accurately predicted the planets' motion as far as astronomers could tell with the instruments available to them. During the Renaissance, however, Nicolaus Copernicus (1473 – 1543), a Polish mathematician and astronomer, proposed a heliocentric, or sun-centered, system. This brought about a conceptual simplication of the solar system, but he was forced to use epicycles to account for retrograde motion as well, and his model was no more accurate than Ptolemy's.

The Copernican model is important chiefly for making possible the formulation of Kepler's Laws of Planetary Motion, which are still taught in courses on celestial mechanics today. They were developed by Johannes Kepler (1571 – 1630), a German mathematician, astronomer, and astrologer, who made use of data collected by Tycho Brahe (1546 – 1601). For us the key point is that Kepler did away with epicycles and deferents by postulating that the planets move in elliptical orbits, with the sun at one focus, and that their speed varies with time according to a simple law.

Here, then, are the laws:

1. Planets move in elliptical orbits around the sun, with the sun at one focus.
2. The focal radius from the sun to the planet sweeps out equal areas over equal times.
3. The square of the orbital period is proportional to the cube of the semimajor axis of the orbit.

The second law implies that each planet moves faster when it is close to the sun and slower when it is far away, as indicated on the diagram to the right. The eccentricity of the orbit is much higher than for any of the planets; comets have such orbits, however. The points indicated on the orbit are equally spaced with respect to time.

Click here for an animation of the planet's motion; click here for a demonstration of the equal-area law. Each of the regions (colored green and yellow in alternation) is swept out over one-twelth of an orbital period, and they all have equal area. The third law states that, if T is the orbital period (the length of the planet's year), and a is the semimajor axis, then

T² = c ⋅ a³

where c is some constant. For instance, in order to octuple the period of the orbit, we must quadruple the semimajor axis.

Kepler's Laws describe how planets move but don't provide any rationale for this. The physical laws proposed by Isaac Newton (1642 – 1727) in his Principia are more universal. His three Laws of Motion are:

1. An object not being subjected to force has constant velocity.
2. The force exerted by a moving object is proportional to the rate of change of the velocity.
3. Every action has an equal and opposite reaction.

His Law of Universal Gravitation is:

• Two objects attract each other with a force proportional to the product of their masses and inversely proportional to the square of their distance.

These four laws can be used to justify Kepler's laws as well as Galileo's laws, if certain simplifying assumptions are made. For instance, Newton's laws imply that the sun and the earth really move around each other; but the sun is so massive compared to the earth that we can consider it as fixed in one place.

We also find that hyperbolic orbits are possible, and obey the equal-area law as well.

Next: Hexagrammum Mysticum