Hexagrammum Mysticum
Let's conclude with a final synthetic result, which we state rather than prove.
Everyone knows that two points determine a line. 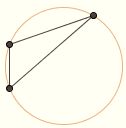 Again, every three noncollinear points determine a circle, the circumcircle of the triangle whose vertices are the three points. Furthermore, the quadrilateral formed by four points on a single circle possesses several special properties, such that the two pairs of opposite sides sum to equal amounts. We shall see how these statements have their analogues in the world of conic sections.
Projective geometry is a branch of geometry in which parallelism plays no role; "infinity" is taken to be a point, and hence lines that are parallel in the usual Euclidean sense meet at this point, so that every pair of lines intersect at some point. Because each line returns to its starting point after passing through infinity, it becomes impossible to speak of one point as being "between" two others, so we lose the concept of betweenness as well. Distance also loses its importance.
 The first true theorem of projective geometry was discovered by Pappus of Alexandria (c.290 – c.350): if the six vertices of a hexagon lie on two lines in alternation, then the three points of intersection for pairs of opposite sides are collinear. Here a "hexagon" is taken as the figure formed by joining six vertices in order, whether or not the "sides" intersect. Notice that line segments have no significance in projective geometry, as we need a concept of betweenness to define them; the sides of the hexagon are lines.
Interest in projective geometry was renewed during the Renaissance through its applications in perspective drawing and architecture. Great artists such as Leonardo da Vinci (1452 – 1519) and Albrecht Dürer (1471 – 1528) wrote books on the mathematics of perspective; the architect Girard Desargues (1591 – 1661) studied nonmetrical geometry and conic sections as well, and has been called the father of projective geometry.
In projective geometry, there is only one type of conic. The distinction between the hyperbola, the parabola, and the ellipse belongs to geometry as we usually conceive of it. We have seen that three noncollinear points determine a circle; similarly, 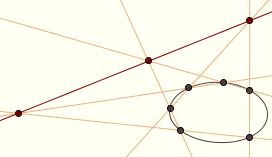 five points in general linear position (meaning that no three points in the set are collinear) determine a conic. Given that a conic is uniquely determined by five points, it seems reasonable to suppose that six points on a single conic bear some special relationship to one another.
This was made concrete by the great mathematician, scientist, and philosopher Blaise Pascal (1623 – 1662) when he was just sixteen. He proved that if a hexagon is inscribed in a conic, then the three points of intersection for pairs of opposite sides are collinear. This theorem is known as the Hexagrammum Mysticum Theorem, and the line through the three points is called the Pascal line. The note in which Pascal states the theorem contains no proof;  it seems likely to have been merely the first step in an extended study of conics, which he never completed. Several synthetic proofs are known, however. A translation of Pascal's paper can be found in David Eugene Smith's Source Book in Mathematics.
A century and a half later, this theorem was "dualized" by the French mathematician Charles Julien Brianchon (1783 – 1864), who proved that, if a hexagon is circumscribed about a conic (with its sides tangent to the conic), its three diagonals are concurrent (meet in a single point). His paper can also be found in A Source Book in Mathematics.
Epilogue
This concludes our tour through the theory of conic sections. I hope you've enjoyed it.
The material formed the basis for a Topics in Mathematics course taught at Rio Grande College in 2012. We began with an overview of Euclidean geometry, emphasizing similarity and Apollonian circles. The main discussion of conics concluded with the derivation of their familiar representations in Cartesian coordinate systems; we then moved on to quadric surfaces.
These pages are humbly dedicated to Robert Miller, my algebra and calculus teacher at Medina Valley High School. I mentioned him in our discussion of satellite dishes. I was a C student in math at the time and had my share of social problems, and if he hadn't taken an interest in me for some inexplicable reason then I would never have dreamed of pursuing math beyond high school. He affected my life in a profound way, though I don't suppose he ever knew it. Requiescat in pace.
Sources |
