Conics are Connected
Our exploration of ellipses, parabolas, and hyperbolas on the previous page may be necessary for an understanding of the subject, but it isn't enough to prove the basic properties we may have guessed at. At this point, from a theoretical point of view, we really know every little about conics.
 For instance, are they connected? If we take a point on one side of a conic, and a second point on the other, does the line segment between them cut the conic, or does it pass through a gap somehow? And what are "sides," anyway? A conic looks like it has an "inside" and an "outside," but how to we characterize these regions in terms of the definition? For instance, are they connected? If we take a point on one side of a conic, and a second point on the other, does the line segment between them cut the conic, or does it pass through a gap somehow? And what are "sides," anyway? A conic looks like it has an "inside" and an "outside," but how to we characterize these regions in terms of the definition?
This is no mere quibble. The very first proposition of Euclid's Elements — the proposition in which he uses the intersection of two circles to construct an equilateral triangle — makes an unspoken assumption not provided for in his axioms, namely, that the two circles actually do intersect. He is assuming, in other words, that a circle is a continuous object. His axioms are insufficient to prove this.
However we choose to remedy this defect in Euclid, in this discussion we'll take the following for granted. The circle of radius r centered at O separates the rest of the plane into two nonoverlapping sets, which we call the interior (the set of all points P such that OP < r) and the exterior (the set of all points P such that OP > r). The following is true of them:
 The interior is a convex set. So, if P and Q are in the interior, then every point of the line segment PQ is in the interior. The interior is a convex set. So, if P and Q are in the interior, then every point of the line segment PQ is in the interior.- If P is in the interior and Q is in the exterior, then the segment PQ cuts the circle exactly once.
- Each line cuts a circle once, twice, or not at all; a line cutting the circle exactly once is called a tangent. If P is in the interior of the circle, then any line through P cuts through the circle exactly twice, once on either side of P.
We'll find that these facts about circles and lines suffice to prove all that we wish concerning the connectedness of conics. For instance, we can show that every line parallel to the directrix cuts the conic once, twice, or not at all. 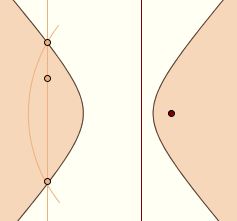 Consider a conic with focus F and directrix l, and let m be a line parallel to l. Let x be the distance between m and l. Any intersection point P between m and the conic satisfies PF = ε ⋅ x, hence lies on the circle of radius εx centered at F. The line m intersects this circle once, twice, or not at all. Consider a conic with focus F and directrix l, and let m be a line parallel to l. Let x be the distance between m and l. Any intersection point P between m and the conic satisfies PF = ε ⋅ x, hence lies on the circle of radius εx centered at F. The line m intersects this circle once, twice, or not at all.
Now we'll say that a point lies in the interior of a conic if the parallel to the directrix intersects the conic twice and the point lies between the two intersection points. A point not in the interior of the conic or on the conic lies in the exterior of the conic.
It turns out that this is equivalent to the following formulation: A point N is in the interior of the conic if the ratio of NF to NS, where S is the foot of the perpendicular to l, is less than ε. To see that these two descriptions amount to the same thing, suppose first that N is in the interior as described above, and let P and Q be the points where the parallel through N intersects the conic. 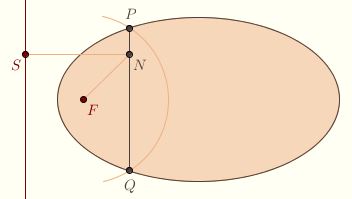 The circle of radius ε ⋅ NS centered at F intersects the line exactly twice, at P and Q, so N is in the interior of the circle, and NF < ε ⋅ NS. Thus NF/NS < ε. The circle of radius ε ⋅ NS centered at F intersects the line exactly twice, at P and Q, so N is in the interior of the circle, and NF < ε ⋅ NS. Thus NF/NS < ε.
On the other hand, if N is a point satisfying NF/NS < ε, then N must be in the interior of the circle of radius ε ⋅ NS, and every line through N intersects the circle exactly twice, once on either side of N. It follows that the parallel to l through N intersects the conic twice, and N is in the interior of the conic.
So far we have only seen that a line parallel to the directrix intersects the conic once, twice, or not at all. However, the same is true of any line, which can be seen as follows. Let m be an arbitrary line in the plane, and suppose that m is not parallel to l. Then they must intersect at a point R.
Suppose we have two points of intersection P and Q between m and the conic. Let p and q be the respective perpendicular distances from these points to l.  The similarity of the triangles implies that PR/QR is equal to p/q. On the other hand, PF/p = ε = QF/q, so p/q = PF/QF. Therefore PR/QR = PF/QF. It follows that the angles made by PF and QF with RF are congruent. If F does not lie on m, then there are at most two such points on m for this angle measure, so m intersects the conic at no other points. The similarity of the triangles implies that PR/QR is equal to p/q. On the other hand, PF/p = ε = QF/q, so p/q = PF/QF. Therefore PR/QR = PF/QF. It follows that the angles made by PF and QF with RF are congruent. If F does not lie on m, then there are at most two such points on m for this angle measure, so m intersects the conic at no other points.
On the other hand, if F does lie on m, then, since QR/QF = PR/PF, R and F divide PQ harmonically in a certain ratio, and m intersects the conic at no other points.
It follows that a line can intersect the conic in at most two points. Conics are therefore of the same "order" as circles.
A line that touches a conic exactly once and contains no point in the interior is called a tangent. A line that intersects a conic in two points is
called a secant. The segment between the two points is called a chord.
Next: The Eccentric Circle |

