The Eccentric Circle
Given a line l, a point F not on l, and ε > 0, we can construct the conic with directrix l, focus F, and eccentricity ε by using an associated circle,
called an eccentric circle of the conic.
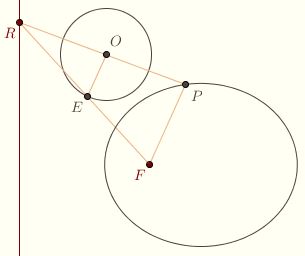 Let O be any point not on l and not equal to F. Let s be its perpendicular
distance from l. Construct the circle with radius ε ⋅ s centered at O. Let E be a point on the circle. If EF is not parallel to l, let R be the point where it intersects l. Let P be the point where the line through F parallel to EO intersects RO, and let p be the distance from P to l. Triangle similarity implies that EO/PF = OR/PR and OP/PR = s/p. So s/p = EO/PF. Now, EO = ε ⋅ s, so PF/p = ε. So P is a point on the conic. Let O be any point not on l and not equal to F. Let s be its perpendicular
distance from l. Construct the circle with radius ε ⋅ s centered at O. Let E be a point on the circle. If EF is not parallel to l, let R be the point where it intersects l. Let P be the point where the line through F parallel to EO intersects RO, and let p be the distance from P to l. Triangle similarity implies that EO/PF = OR/PR and OP/PR = s/p. So s/p = EO/PF. Now, EO = ε ⋅ s, so PF/p = ε. So P is a point on the conic.
On the other hand, if EF is parallel to l, let P and p be as before. Note that p = s. Quadrilateral EFPO is a parallelogram, so PF = EO. It follows that PF/p = EO/s = ε. So P is on the conic.
The idea is that, as E travels around the circle, P sweeps out the conic. Click here to see an animation of the ellipse being swept out; click here to see an animation of the hyperbola.
We discover the following:
- If the conic is an ellipse, then the directrix does not intersect the eccentric circle.
- If the conic is a parabola, then the directrix is tangent to the eccentric circle.
- If the conic is a hyperbola, then the directrix intersects the eccentric circle exactly twice, and the two parts of the circle correspond to the two branches of the hyperbola.
 The beauty of the eccentric circle construction is that it allows us to translate well-known properties of the circle into properties of conics. For instance, from any point in the exterior of a circle, there exist exactly two lines tangent to the circle. This allows us to prove that, from any point in the exterior of a conic (where exterior is defined as in the previous section), there exist exactly two lines tangent to the conic. The beauty of the eccentric circle construction is that it allows us to translate well-known properties of the circle into properties of conics. For instance, from any point in the exterior of a circle, there exist exactly two lines tangent to the circle. This allows us to prove that, from any point in the exterior of a conic (where exterior is defined as in the previous section), there exist exactly two lines tangent to the conic.
To see this, let O be any point in the exterior of the conic. Construct the eccentric circle centered at O. There are exactly two tangents m and n from F to the eccentric circle. Use them to obtain points P and Q on the conic. 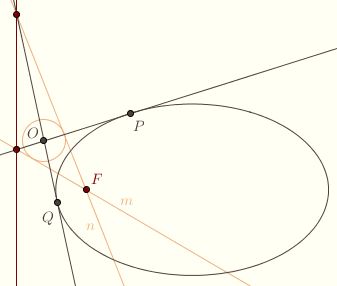 It remains to show that OP and OQ are tangent to the conic. It remains to show that OP and OQ are tangent to the conic.
Note that PF is perpendicular to m. Let T be any point on OP other than P. Let t be the distance from T to the directrix, and s the distance from T to m. Then s/t = ε. On the other hand, TF > s since the shortest distance from T to m is along
the perpendicular, so TF/t > ε. It follows that T is in the exterior of the
conic. So OP is tangent to the conic. Similarly for OQ. This establishes that there are at least two tangents from O to the conic.
On the other hand, each tangent from O to the conic produces a tangent from F to the eccentric circle, and there are only two such, so the tangents
just constructed are the only tangents possible.
If O happens to be on l, then it is not possible to construct the eccentric circle. 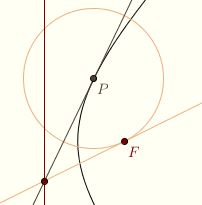 The points of tangency are the points where the line perpendicular to OF at F intersects the conic. This is not difficult to prove. The points of tangency are the points where the line perpendicular to OF at F intersects the conic. This is not difficult to prove.
The fact that there is exactly one tangent to any point on a conic follows similarly. Let P be a point on the conic. The eccentric circle centered at P is the circle passing through F. There is exactly one tangent to the circle at F. Use this to produce a tangent to the conic.
This establishes existence. On the other hand, given a tangent at P, the
reverse of this operation produces a tangent to the circle at F, of which
there is exactly one. This establishes uniqueness.
Next: Conic Diameters |

